Post

ETC - 정렬 알고리즘

ETC

Posted Updated
By SJH
10 min read
ETC - 정렬 알고리즘

정렬 알고리즘

오늘은 5가지 정렬에 대해 공부해봤다.

버블 정렬

현재 가장 적합한 값을 배열의 끝으로 이동시키는 알고리즘

작동 원리

  1. 배열의 첫 번째 요소부터 시작해 인접한 두 요소 비교
  2. 정렬 순서에 맞게 교환
  3. 루프가 한 번 끝나면, 가장 큰(작은) 값이 맨 뒤로 이동
  4. 배열의 크기만큼 반복

특징

  • 구현이 쉽다.
  • 시간 복잡도
    • 최선 O(n)
    • 평균 O(n^2)
    • 최악 O(n^2)
  • 공간 복잡도
    • 추가 메모리 사용이 거의 없음
  • 효율성
    • 소규모 데이터셋에는 적절, 대규모에선 비효율적

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

void BubbleSort(vector<int>& v) // 버블 정렬
{
	size_t size = v.size();

	for (size_t i = 0; i < size - 1; i++)
	{
		for (size_t j = 0; j < size - i - 1; j++)
		{
			if (Compare(v[j], v[j + 1]))
			{
				Swap(v[j], v[j + 1]);
			}
		}
	}
}

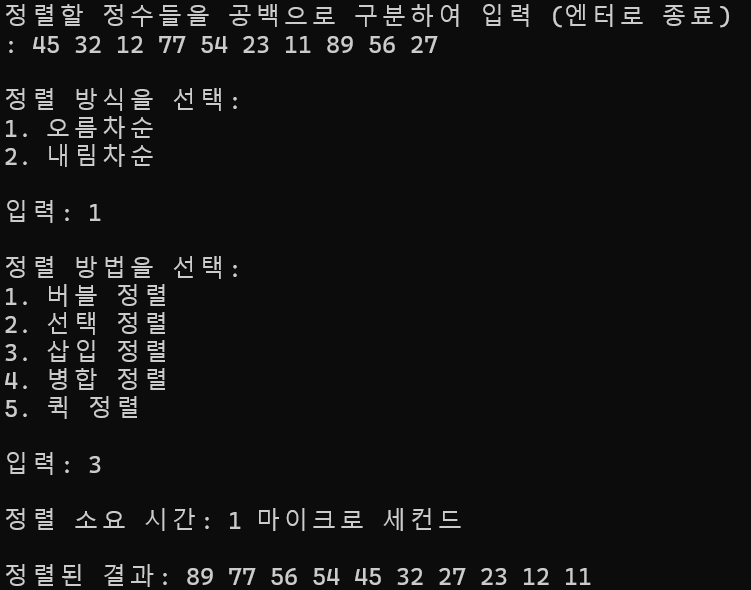
10개 정렬

10개 정렬

정렬 소요 시간 : 2ms

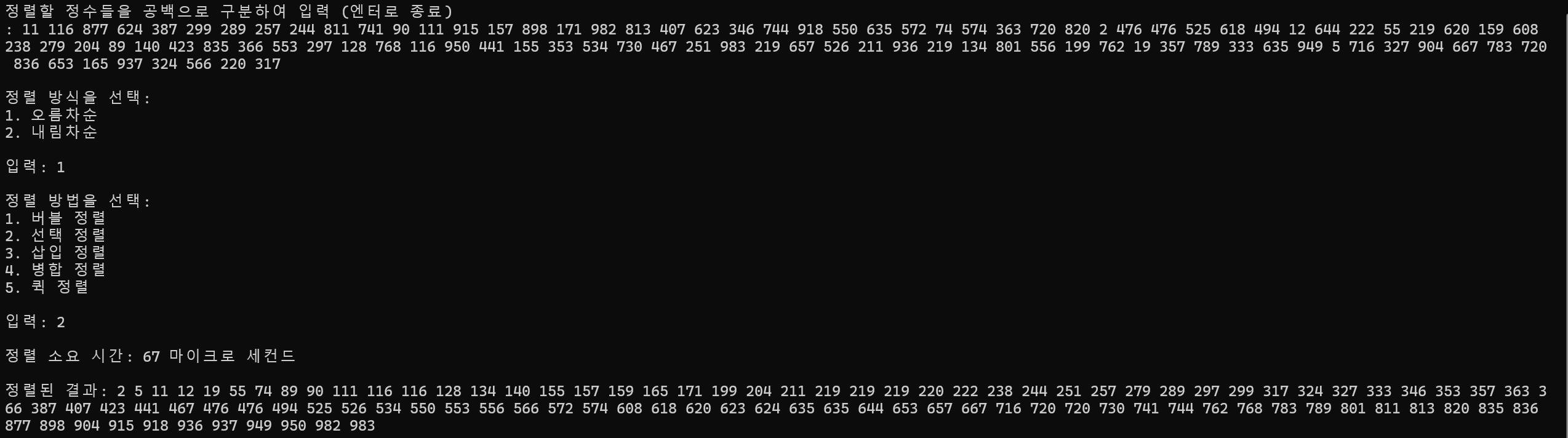
100개 정렬

100개 정렬

정렬 소요 시간 : 96ms

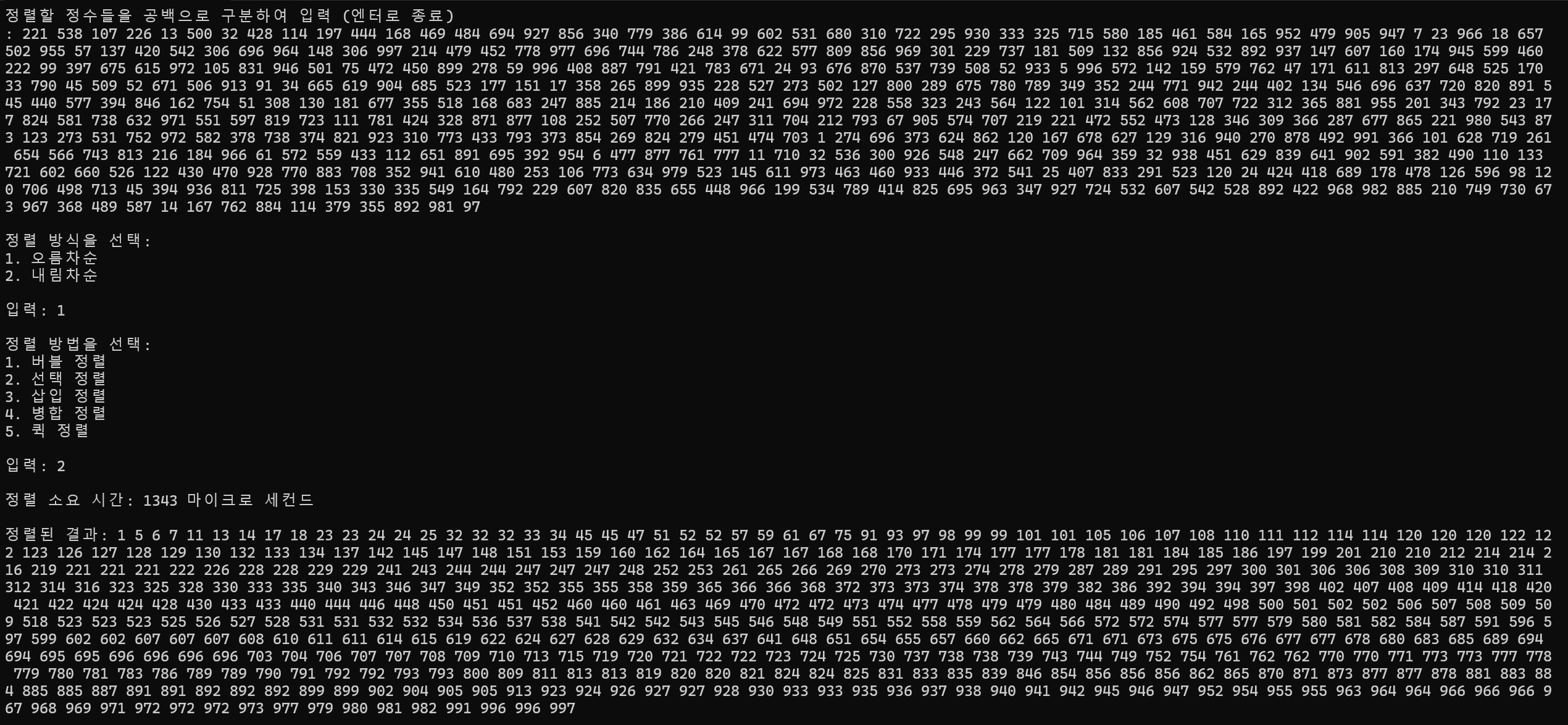
500개 정렬

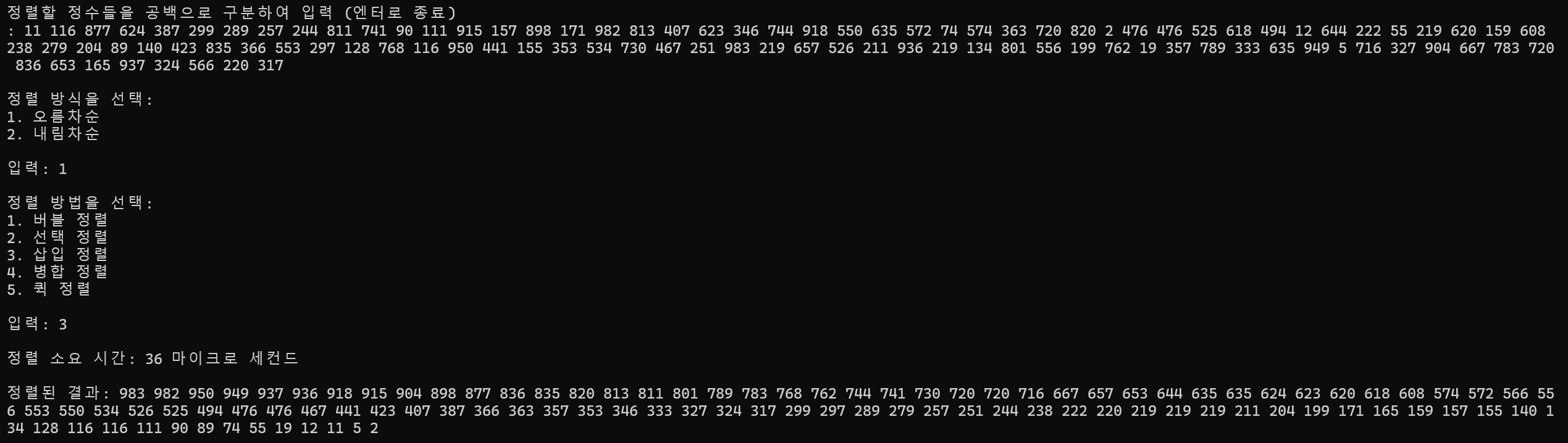
500개 정렬

정렬 소요 시간 : 1694ms

선택 정렬

하나의 값을 선택해, 가장 적합한 자리로 이동시키는 알고리즘

작동 원리

  1. 정렬되지 않은 부분에서 맨 앞 요소 선택
  2. 자신 뒤의 값들을 순회하며 크기 비교
  3. 적합한 자리(가장 작거나 큰 값)를 찾으면 정지 후 스왑
  4. 위 동작을 배열 크기 - 1 만큼 반복

특징

  • 역시 구현이 쉽다.
  • 시간 복잡도
    • 최선 O(n^2)
    • 평균 O(n^2)
    • 최악 O(n^2)
  • 공간 복잡도
    • 추가 메모리 사용이 거의 없음
  • 효율성
    • 어떤 경우에서도 O(n^2) 이기에, 데이터셋이 커질 수록 효율이 나빠진다.

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

void SelectionSort(vector<int>& v) // 선택 정렬
{
	size_t size = v.size();

	for (size_t i = 0; i < size - 1; i++)
	{
		int index = i;

		for (int j = i + 1; j < size; j++)
		{
			if (Compare(v[index], v[j]))
			{
				index = j;
			}
		}

		Swap(v[i], v[index]); // i == index 면 낭비지만 어짜피 데이터셋이 크면 사용하지 않을 것이니니 pass
	}
}

10개 정렬

10개 정렬

정렬 소요 시간 : 1ms

100개 정렬

100개 정렬

정렬 소요 시간 : 67ms

500개 정렬

500개 정렬

정렬 소요 시간 : 1343ms

삽입

정렬되지 않은 부분에서 하나의 요소를 선택해 정렬된 부분에 삽입하는 방식

작동 원리

  1. 두 번째 요소부터 시작해 이전 요소들과 비교
  2. 올바른 위치를 찾아 삽입
  3. 위 과정을 배열의 끝까지 반복

특징

  • 같은 값끼리 상대적 위치를 유지할 수 있다. (안정적인 정렬 알고리즘이다)
  • 시간 복잡도
    • 최선 O(n)
    • 평균 O(n^2)
    • 최악 O(n^2)
  • 공간 복잡도
    • 추가 메모리 사용이 거의 없음
  • 효율성
    • 거의 정렬된 데이터에 적합, 역시 큰 데이터셋에선 사용하기 비효율적

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

void InsertionSort(vector<int>& v)
{
	size_t size = v.size();

	for (size_t i = 1; i < size; i++)
	{
		int key = v[i];
		int j = i - 1;

		while (j >= 0 && Compare(key, v[j])) //여긴 Swap 보단 뒤로 밀어내는 게 효율이 좋음
		{
			v[j + 1] = v[j];
			j--;
		}

		v[j + 1] = key;
	}
}

10개 정렬

10개 정렬

정렬 소요 시간 : 1ms

100개 정렬

100개 정렬

정렬 소요 시간 : 36ms

500개 정렬

500개 정렬

정렬 소요 시간 : 767ms

합병

분할 정복 방식의 대표적인 예시로, 배열을 반복적으로 반으로 나누고 각각을 정렬하고 병합하여 정렬하는 방식이다.

작동 원리

  1. 분할
    • 배열을 두 개의 부분 배열로 나누어, 더 이상 나눠지지 않을 때 까지 반복
  2. 정복
    • 각 부분 배열이 길이가 1이 되면, 정렬된 상태이므로 두 배열을 정렬된 방식으로 병합
  3. 병합
    • 두 개의 정렬되 배열을 차례대로 크기 비교해 새로운 배열에 삽입
    • 이 때, 한쪽 배열이 다 비면 다른 배열을 그 뒤에 바로 삽입하면 된다.

특징

  • 구현이 다소 복잡함
  • 안정적인 정렬 알고리즘
  • 시간 복잡도
    • 최선 O(n log n)
    • 평균 O(n log n)
    • 최악 O(n log n)
  • 공간 복잡도
    • 배열을 나누고 병합하며 O(n)의 공간을 추가로 요구
  • 매우 큰 배열을 다룰 때 효율적

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

void Merge(vector<int>& v, const int left, const int mid, const int right)
{
	int leftSize = mid - left + 1;
	int rightSize = right - mid;

	vector<int> leftVector(leftSize), rightVector(rightSize);

	for (int i = 0; i < leftSize; i++)
	{
		leftVector[i] = v[left + i];
	}

	for (int i = 0; i < rightSize; i++)
	{
		rightVector[i] = v[mid + 1 + i];
	}

	int leftIndex = 0, rightIndex = 0, curIndex = left;
	
	while (leftIndex < leftSize && rightIndex < rightSize)
	{
		if (Compare(rightVector[rightIndex], leftVector[leftIndex]))
		{
			v[curIndex++] = leftVector[leftIndex++];
		}
		else
		{
			v[curIndex++] = rightVector[rightIndex++];
		}
	}

	while (leftIndex < leftSize)
	{
		v[curIndex++] = leftVector[leftIndex++];
	}
	while (rightIndex < rightSize)
	{
		v[curIndex++] = rightVector[rightIndex++];
	}

}

void MergeSort(vector<int>& v, int left, int right)
{
	if (left < right)
	{
		int mid = left + (right - left) / 2; // 오버플로우 방지

		MergeSort(v, left, mid);
		MergeSort(v, mid + 1, right);

		Merge(v, left, mid, right);
	}
}

10개 정렬

10개 정렬

정렬 소요 시간 : 20ms

100개 정렬

100개 정렬

정렬 소요 시간 : 152ms

500개 정렬

500개 정렬

정렬 소요 시간 : 677ms

퀵

이것도 분할 정복 알고리즘으로 피벗을 기준으로 배열을 두 개로 나누어 정렬하는 방식을 사용한다.

동작 방식

  1. 피벗 선택 (배열의 첫 번째, 중앙, 랜덤 위치 아무거나 상관없음) 피벗을 선택하지 못하면 return
  2. 피벗을 기준으로 작은 값과 큰 값을 배치 (오름차순에선 작은 게 피벗 왼쪽, 큰 게 피벗 오른쪽)
  3. 피벗은 이제 올바른 위치에 있으므로, 피벗을 제외한 2개의 부분 배열을 위 방식 그대로 반복

특징

  • 같은 값끼리의 원소 순서를 보장하지 않는 불안정 정렬
  • 피벗을 잘못 선택하는 경우 최악의 시간 복잡도를 가지게 된다.
  • 시간 복잡도
    • 최선 O(n log n)
    • 평균 O(n log n)
    • 최악 O(n^2)
  • 공간 복잡도
    • O(log n) (재귀 함수 호출 말고는 추가 메모리 사용이 없음)

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

int Quick(vector<int>& v, int left, int right)
{
	// 맨 끝이 피벗, i 왼쪽에 배치할 자리
	int pivot = v[right];
	int leftIndex = left - 1;
	
	for (int rightIndex = left; rightIndex < right; rightIndex++) //왼쪽부터 순회하며 피벗과 비교
	{
		if (!Compare(v[rightIndex], pivot))
		{
			Swap(v[++leftIndex], v[rightIndex]); //기준 왼쪽에 기준 미달 넣기
		}
	}

	Swap(v[leftIndex + 1], v[right]); // 피벗 오른쪽엔 조건 성립한 애들이 있어야함

	return leftIndex + 1; //피벗 위치 반환
}

void QuickSort(vector<int>& v, int left, int right)
{
	if (left < right)
	{
		int pivotIndex = Quick(v, left, right);

		QuickSort(v, left, pivotIndex - 1);
		QuickSort(v, pivotIndex + 1, right);
	}
}

10개 정렬

10개 정렬

정렬 소요 시간 : 1ms

100개 정렬

100개 정렬

정렬 소요 시간 : 12ms

500개 정렬

500개 정렬

정렬 소요 시간 : 84ms

ETC
ETC
This post is licensed under CC BY 4.0 by the author.